Past Research
Direct Measurement of the
Wavefunction
| Chosen
as 2nd most important Physics
Breakthrough of 2011 by
Physics World! Central to quantum theory, the wavefunction is a complex distribution associated with a  quantum
system. Despite its fundamental role, it is typically
introduced as an
abstract element of the theory with no explicit definition.
Rather,
physicists come to a working understanding of it through its
use to
calculate measurement outcome probabilities through the Born
Rule.
Tomographic methods can reconstruct the wavefunction from
measured
probabilities. In contrast, we demonstrated a method to
directly
measure the wavefunction so that its real and imaginary
components
appear straight on our measurement apparatus. At the heart
of the
method is a joint measurement of position and momentum that
is made
possible by weak measurement (see
below
for what that is).
As an example of the method we experimentally directly
measured the
transverse spatial wavefunction of a single photon. This new
measurement gives the wavefunction a plain and general
meaning in
terms of a specific set of operations in the lab. quantum
system. Despite its fundamental role, it is typically
introduced as an
abstract element of the theory with no explicit definition.
Rather,
physicists come to a working understanding of it through its
use to
calculate measurement outcome probabilities through the Born
Rule.
Tomographic methods can reconstruct the wavefunction from
measured
probabilities. In contrast, we demonstrated a method to
directly
measure the wavefunction so that its real and imaginary
components
appear straight on our measurement apparatus. At the heart
of the
method is a joint measurement of position and momentum that
is made
possible by weak measurement (see
below
for what that is).
As an example of the method we experimentally directly
measured the
transverse spatial wavefunction of a single photon. This new
measurement gives the wavefunction a plain and general
meaning in
terms of a specific set of operations in the lab. |
For
the non-physicists here are
a
Semi-technical explanation and
 Non-technical
explanation of the idea. For physicists, here
is video of presentation I gave along with the slides. Non-technical
explanation of the idea. For physicists, here
is video of presentation I gave along with the slides.Briefly, the idea is as follows: The average result of a weak measurement of A on state psi and which is then strongly measured to be in state phi is called the weak value. It is given by A_w on the right. Weakly measuring the projector |x><x| followed by a strong measurement with result p=0 results in a weak value proportional to the wavefunction. |
How
the experiment works: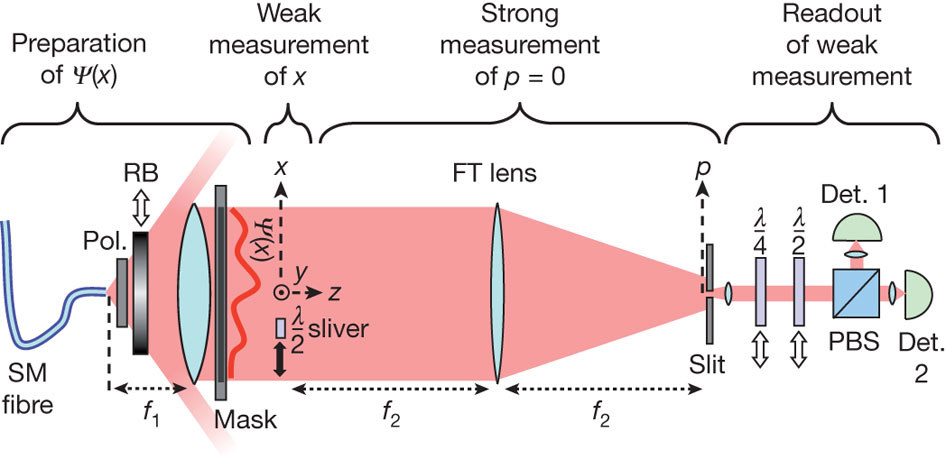 1. Produce a collection of photons possessing identical spatial wavefunctions by passing photons through an optical fiber. 2. Weakly measure the transverse position by inducing a small polarization rotation at a particular position, x. 3. Strongly measure the transverse momentum by using a Fourier Transform lens and selecting only those photons with momentum p=0. 4. Measure the average polarization rotation of these selected photons. This is proportional to the real part of the wavefunction at x. 5. Measure the average rotation of the polarization in the circular basis. (i.e. difference in the number of photons that have left-hand circular polarization and right-hand circular polarization). This is proportional to the imaginary part of the wavefunction at x. 6. Repeat for all x to scan through the wavefunction. |
Engineering Sources of
Single Photons
|
Quantum dot sources of
single-photons and entangled photon pairs have the |
|
Another,
more common single
photon source is spontaneous parametric downconversion. 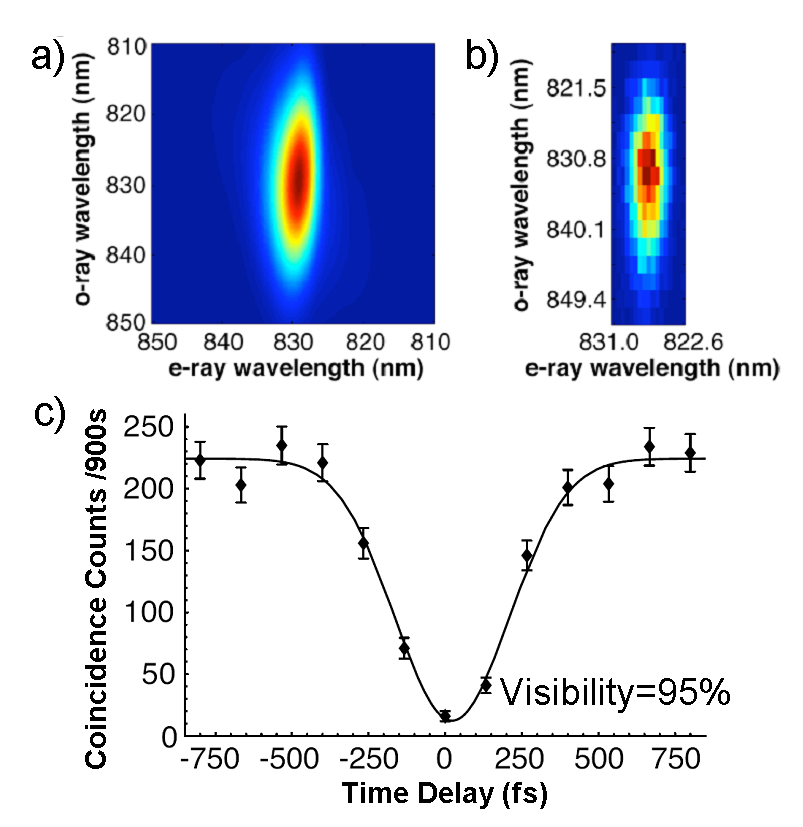 This
process produces photons in pairs. Thus, the detection of on
photon
heralds its twin. At Oxford University, we developed and
demonstrated a
heralded single-photon source that is unique in producing
photons in a
pure spectral-temporal state (i.e. without time or frequency
jitter). The key to this was eliminating spectral
correlations
between the two photons in the pair. a) and b) show the
theoretical and
experimental joint spectra, which exhibit no correlations.
Eliminating
spectral filtering allow us to achieve one of the best
photon
generation rates in the field, we also observed the highest
quality
multi-photon interference yet described in the literature
(see Figure
c)). Photon quantum logic gates function via this
interference and it
is currently the limiting factor in their functioning. In
addition, the
ability to build tailored multi-photon states from single
photons
relies on the photons being in pure quantum states. This
process produces photons in pairs. Thus, the detection of on
photon
heralds its twin. At Oxford University, we developed and
demonstrated a
heralded single-photon source that is unique in producing
photons in a
pure spectral-temporal state (i.e. without time or frequency
jitter). The key to this was eliminating spectral
correlations
between the two photons in the pair. a) and b) show the
theoretical and
experimental joint spectra, which exhibit no correlations.
Eliminating
spectral filtering allow us to achieve one of the best
photon
generation rates in the field, we also observed the highest
quality
multi-photon interference yet described in the literature
(see Figure
c)). Photon quantum logic gates function via this
interference and it
is currently the limiting factor in their functioning. In
addition, the
ability to build tailored multi-photon states from single
photons
relies on the photons being in pure quantum states. |
|
|
The
crucial design element in
the source above is the control of momentum |
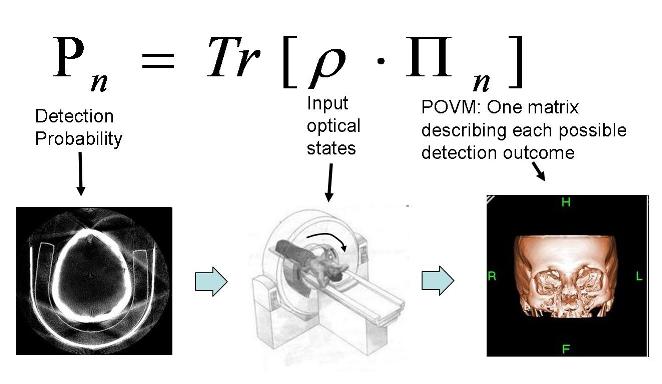
Measuring Measurement: Tomography of detectors
|
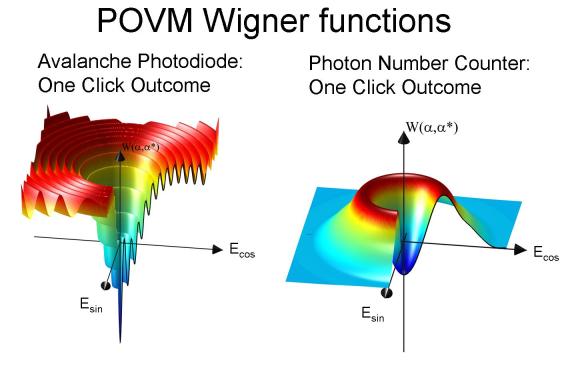
Measurement plays an important role in quantum physics, causing the collapse of the wavefunction. Yet, given a particular device, how do we know what measurement it actually does? Using the technique of tomography, for the first time we reconstruct a full “image” of the measurement a detector performs. Tomography is used, for example, in CAT scans, reconstructing full three-dimensional images of the body by taking a series of two-dimensional pictures from different angles. A generalization of this idea allows us to reconstruct the measurement performed by a new type of quantum detector that can count photons. |
 |
| Despite our belief that quantum physics should describe everything, the measurement process itself cannot be rigorously modeled by quantum dynamics alone. We approach this problem from the opposite direction with a general procedure for characterizing a detector by the information it gives us. Remarkably, this finite set of information is enough to predict the detector’s response to any possible input. We successfully characterized a photon number counting detector, an exciting new device at the ultimate limit of light detection. |  |
| The tomography
procedure: 1. Create a series of coherent states with different intensities. 2. Measure the intensities of the coherent states with the power meter in a monitor arm. 3. For each intensity measure the rates of each detector outcome. 4. These rates allow us to reconstuct the set of matrices describing the detector action (The detector POVM). The Wigner functions on the right depict the POVM element for the one click outcome of an Avalanche Photodiode and a Photon Number Resolving Detector. |
 |
Single-photon nonlinearities
|
Entanglement and interference are often identified as two of the defining phenomena of quantum physics. Quantum computation algorithms rely on both to perform classically impossible tasks such as factoring large numbers. In these algorithms entanglement is created in two-particle quantum logic gates, but in optics we don't have a strong enough interaction (nonlinearity) between photons to create these. Can quantum interference be used as the nonlinear interaction in a quantum gate? Usually, the answer appears to be no. In a series of experiments, we show that interference can be used to enhance a pre-existing nonlinearity by eleven orders of magnitude up to the level where single photons can scatter from each other. |
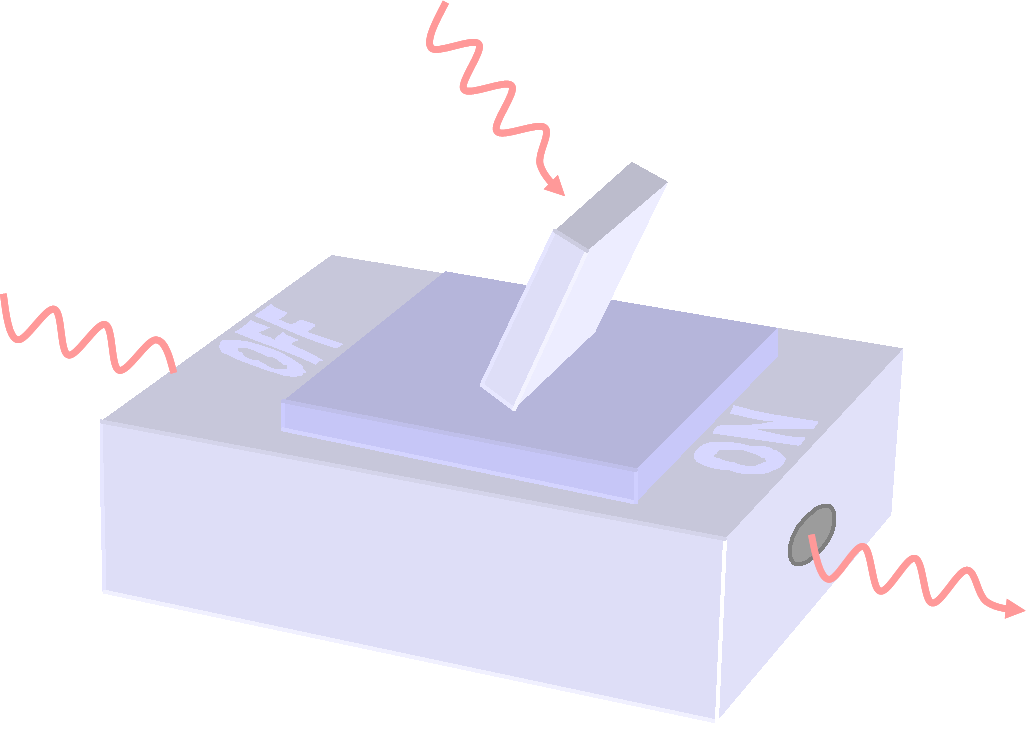 |
| In
two experiments, spontaneous
parametric
down-conversion is suppressed or enhanced by interference
with two
photons from
a classical local-oscillator field. When there is
destructive
interference, any
photon pairs from the laser fields undergo sum-frequency
generation and
are
removed from the beams. In this sense, there is an effective
two-photon
nonlinearity that is significant even when only two photons
are present
at a
time. While the
underlying physics is
that of incipient two-mode squeezing, it comprises
qualitatively new
effects
when studied at the single-photon level.
For instance, it functions essentially as an absorptive
two-photon switch. If the phase of
the pump is shifted
relative to the
incoming photons, then it functions similar to a conditional-phase
quantum logic
gate;
if and only if both photons are present will the output
state be
shifted in phase. We have found uses for these effects in
a
universal Bell-state analyzer and in Hardy's Paradox (see
below). |
 |
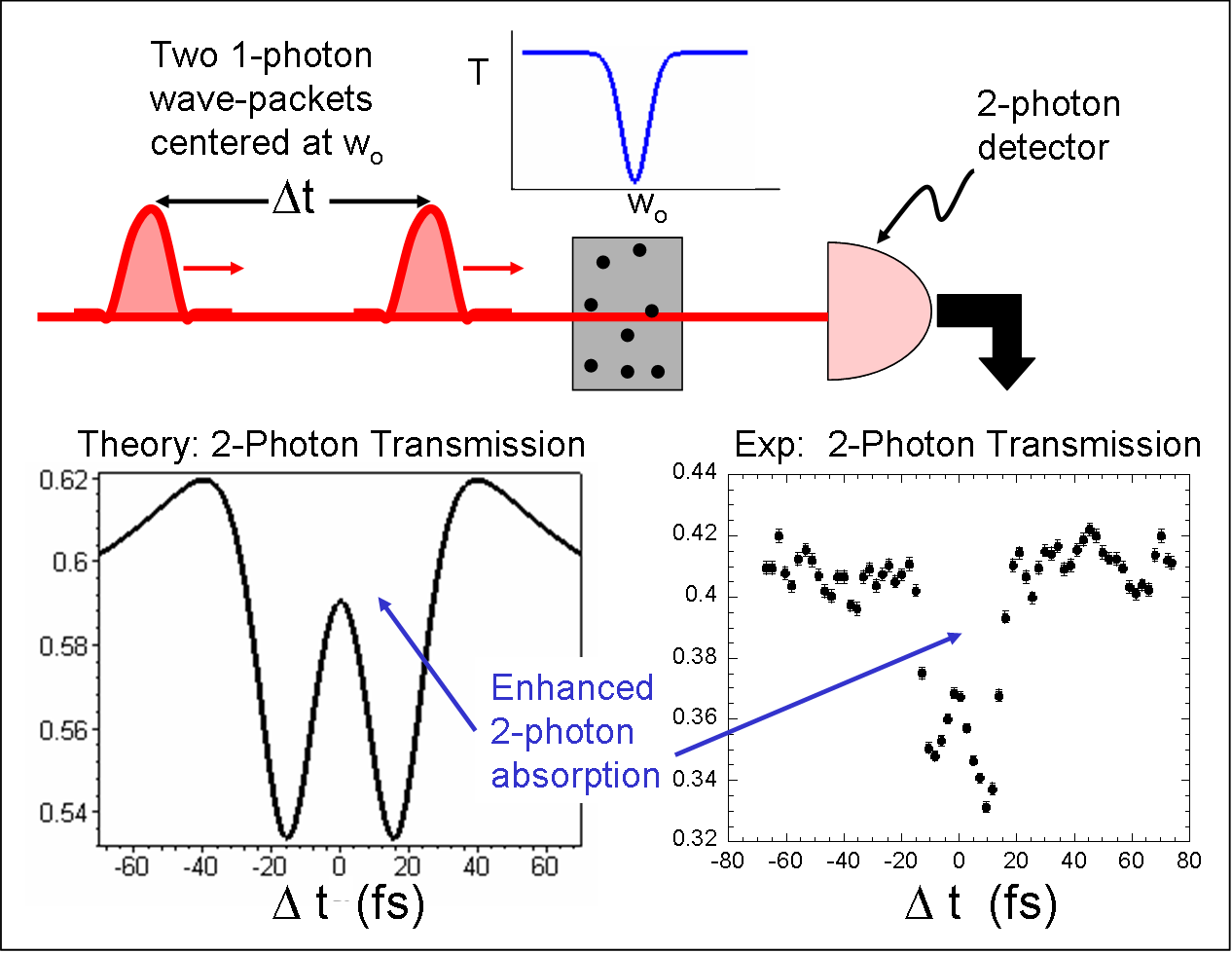
| In
a third experiment, we show
that exchange effects, responsible for Pauli exclusion among
other
things, can modify photon-photon interactions from what
would be
predicted for distinguishable particles. In collaboration
with
Geoff Lapaire and John Sipe, we demonstrate an exchange
effect with two
single-photon states that involves real transitions in
media.
Interference occurs between the two paths in which both
photons can be
absorbed. When the photons are completely overlapped or
completely separated in time, the absorption is that of two
distinguishable particles. But for intermediate times, the
absorption is unexpectedly suppressed as if there was an
effective
interaction between the two photons. |
 |
Measurement in quantum mechanics
Weak Measurement
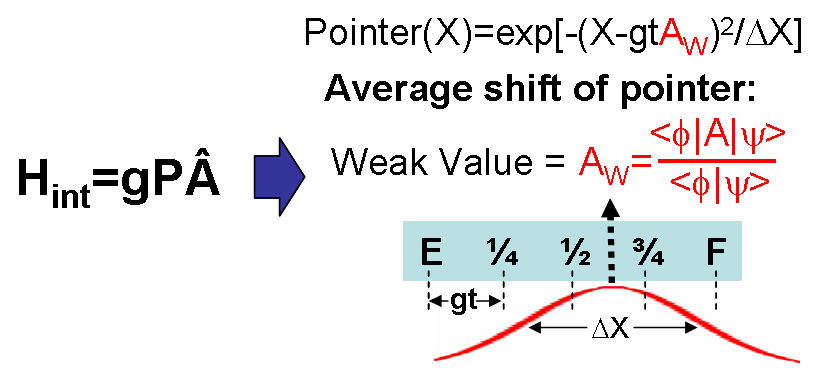
| Weak
measurement was originally proposed by Aharanov,
Albert and Vaidman as
an extension to the
standard
von Neumann ("strong") model of measurement.
A weak measurement can be performed by
sufficiently reducing the coupling between the measuring
device and the
measured system. In
this case, the
pointer of the measuring device begins in a state with
enough position
uncertainty that any shift induced by the weak coupling is
insufficient
to distinguish
between the eigenvalues
of the observable
in a single
trial. While
at first glance it may
seem strange to desire a measurement technique that gives
less
information than
the standard one, recall that the entanglement generated
between the
quantum
system and measurement pointer is responsible for collapse
of the wavefunction.
Furthermore, if multiple trials are performed on an
identically-prepared
ensemble of systems, one can measure the average shift of
the pointer
to any
precision -- this average shift is called the weak value. A surprising
characteristic of weak values is
that they need not lie within the eigenvalue
spectrum
of the observable and can even be complex.
On the other hand, an advantage of weak measurements
is
that
they do not
disturb the measured system nor any other simultaneous weak
measurements or
subsequent strong measurements, even in the case of
non-commuting
observables. This
makes weak
measurements ideal for examining the properties and
evolution of
systems before post-selection and
might enable the
study of new types of observables.
Weak
measurements have been used to simplify the calculation of
optical
networks in
the presence of polarization-mode dispersion by Gisin,
applied to slow- and fast-light effects in birefringent
photonic crystals by Chiao,
and bring a
new, unifying
perspective to the tunneling-time controversy as Steinberg
showed. Wiseman used weak values
to physically
explain the results of a cavity QED experiment.
Weak measurement can be considered the best estimate
of an
observable in
a pre and post-selected system. |
 |
Interaction-Free Measurement
| This is a type of measurement proposed by Elitzur and Vaidman in 1991 in which the presence of an object can be discerned without it being disturbed. The simplest example of this type of measurement is a Mach-Zehnder interferometer (shown to the right) that is aligned so that all the photons entering the interferometer leave through the "bright" output port C (and none through D, the "dark" output port). Both the first and last beam splitters (BS1 and BS2) reflect and transmit with 50% probability. Consider what would happen if an object, say a highly light-sensitive bomb, were positioned in the right-hand path (I). If we let only one photon enter the interferometer, it has a 50% chance of taking the left path (O), thus avoiding triggering the bomb. It then has a 50% chance of exiting through port C, which conveys no information about the presence of the bomb, and a 50% chance of exiting through the previously dark port, D. The latter then indicates the presence of the bomb even though the photon did not interact with it. In total, one has a 25% chance of success (detecting the bomb without detonating it), 25% chance of receiving no knowledge and a 50% chance of failure (an explosion). We setup two Interaction-Free Measurements of this type in our lab to show that sometimes their results can be in contradiction to what any reasonable person would logically expect (see Hardy’s Paradox below). | 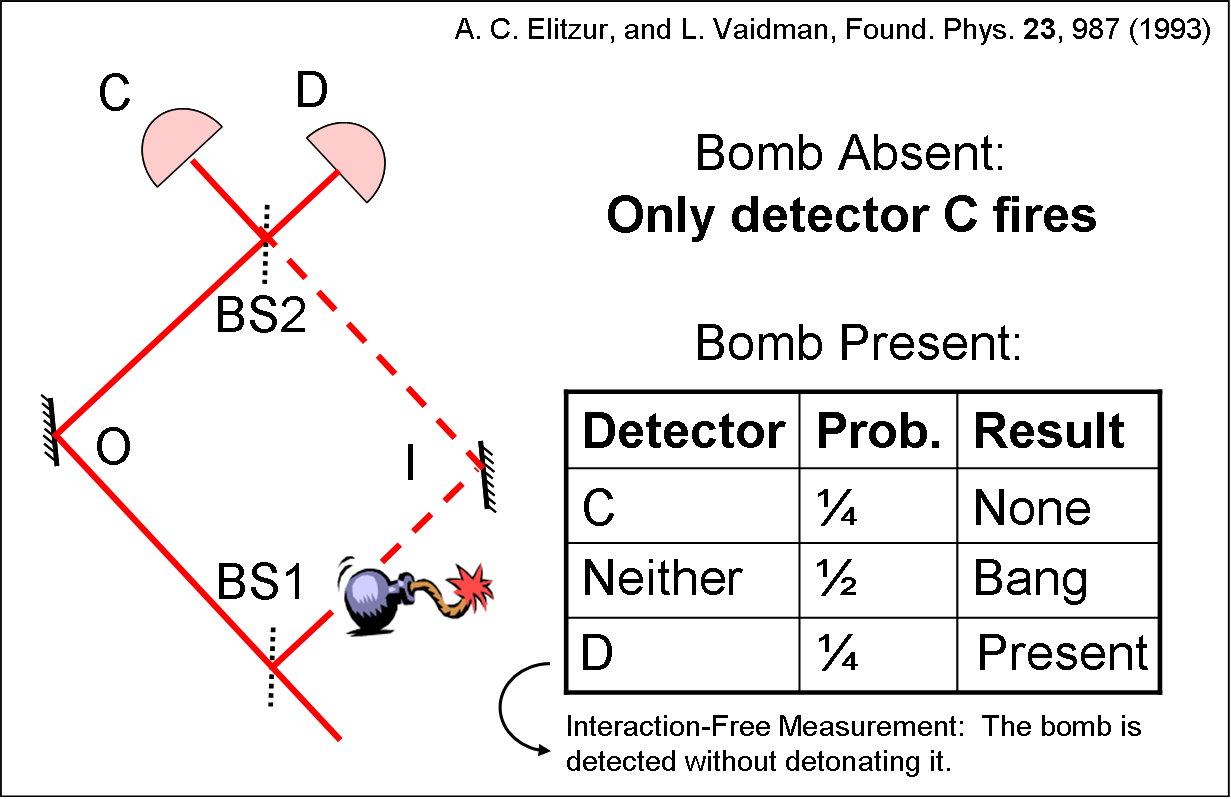 |
A logical paradox in quantum mechanics
Interaction-Free Measurement continued
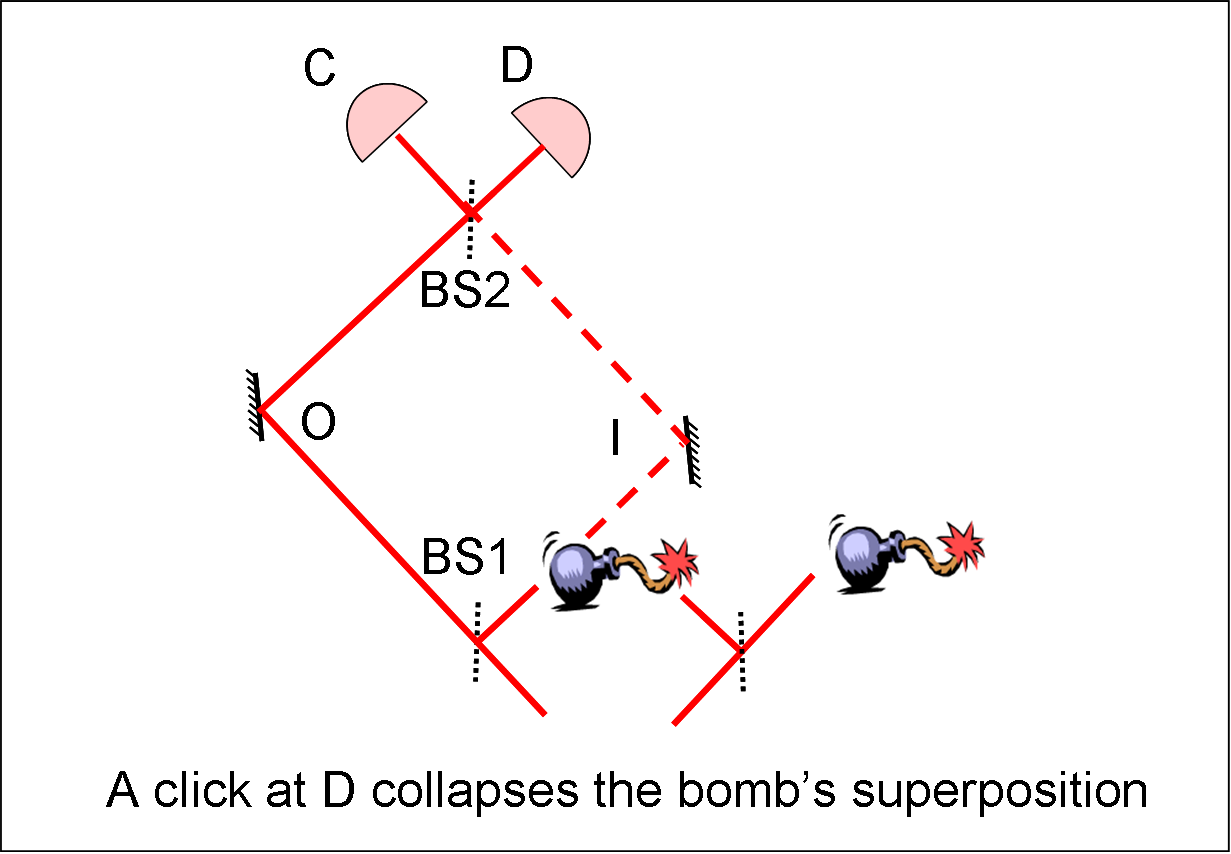
| The above
analysis of
Interaction-Free Measurement (IFM) naturally
leads one to
the question of whether the photon was in the bomb arm in
trials which
were
successful. If not, how could the bomb's presence influence
which
output
port the photon took. If so, why did the bomb not explode
and
how
did the
photon get to the detector? As the next step towards Hardy's
Paradox, consider what would happen if the bomb were in an
equal
superposition
of two position states, one in the arm I and one outside of
the
interferometer? In this scenario, if a photon is detected
in
the
dark
port D, the state of the bomb
collapses to
a state in
the arm I. On the other hand, if the photon exits from the
bright
port C,
no collapse occurs. Evidently, IFM's
can also
detect objects which exhibit wave-like properties such as a
superposition of
states.
|
 |
Hardy's Paradox
| Hardy's
Paradox takes this scenario one step further.
Lucien Hardy envisioned using an electron as the test
particle in the
IFM and a
positron as the bomb (see Figure 2). The positron
is placed
into a
superposition by a 50/50 beamsplitter.
The
extra
step is that after the electron and positron would have
annihilated each
other in region W, the positron superposition is recombined
at another
50/50 beamsplitter.
We now have a
symmetric experiment
where both the electron and positron enter Mach-Zehnder
interferometers (distinguished by the subscripts - and +
respectively).
Each interferometer performs an IFM on the particle in the
other
interferometer. |
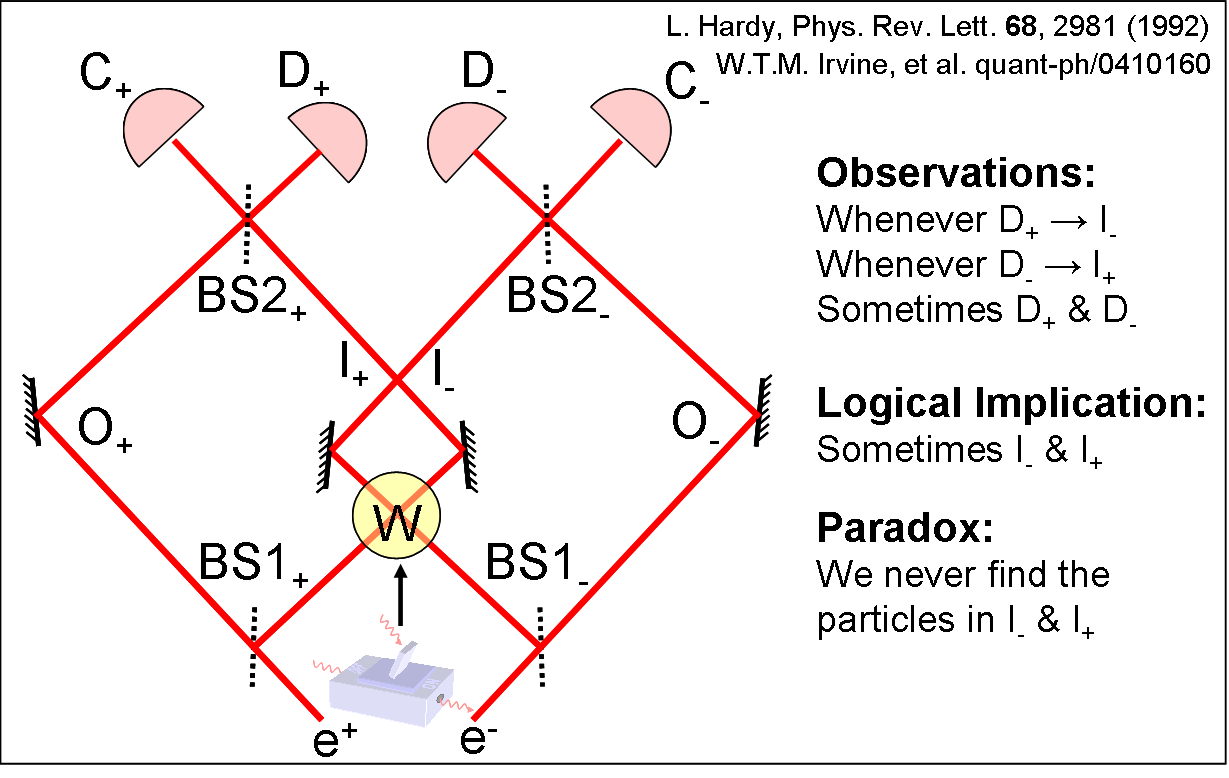 |
| If one detects the electron at D₋ this implies that the positron was in I₊ and conversely, a positron at D₊ implies the electron was in I₋. Surprisingly, it is possible for both the electron and positron to exit their respective D port in the same trial, implying they were each in their respective I arm. Consequently, this appears to answer the question in the last section of which arm the electron was in before a successful measurement: The arm with the object in it. But then how did the electron and positron avoid annihilation and yet arrive at our detectors?. These two contradictory conclusions arise from the false classical idea that a particle has determinate properties, such as position, before observation. This is the essence of Hardy's Paradox and the form of it that experimentally implement. Instead of electron, and positron we use H and V polarized photons and we use an absorptive two-photon switch in region W (see above). |  |
Weak Measurement in Hardy's Paradox
|
The IFM dark port detections only allow us to make counterfactual claims about which MZI arms the photons were in. Any strong measurements designed to verify these claims would disturb at least one of the MZIs, so that it would no longer act as an IFM. Thus the paradox would be destroyed. On the other hand, because they do not disturb the system, weak measurements can test these claims. Aharonov et al. used weak measurement to find which Mach-Zehnder arms the photons were in, individually and as a pair, in the subensemble of systems for which the IFMs give their paradoxical result. The resulting weak values for the single-photon occupation numbers (eg. |O+>< O+|) were found to be NO+ = 0, NO- = 0, NI+ = 1, NI- = 1, where I is the inner arm and O is the outer arm. These simply agree with the results of the IFMs: Individually, the photons were in the inner arms. However, the impossibility of detecting two photons which were both in the inner arms (they would have “annihilated”) means that NI,I =0. From this we find that NO,I and NI,O equal one since we already know 1= NI+ = NI,I + NI,O for instance. But since we know neither photon was in the outer arms, 0= NO+ = NO,I + NO,O, implying the strange result NO,O = –1. We experimentally implemented the proposed weak measurements using a small polarization rotation θ in the relevant arm(s). In particular, we found that when weakly measuring NO,O the photons emerged at the dark ports with a polarization rotated in the opposite direction from what the rotation θ, we imposed. The exact measurement came out to roughly NO,O = –0.75.
|
 |
Super-resolving measurements
| Resolution is a limiting factor for many scientific endeavors. For example, electron microscopes can see smaller objects than light microscopes because they have higher resolution. This paper describes a way to break through some resolution limits using quantum-mechanical entanglement. By entangling three photons in the state |30>+|03>, we were able to increase their resolution threefold over the single-photon limit. This concept in general entails creating a quantum state containing N photons, where the N photons are always found together in one interferometer arm or the other, sometimes called a "high-noon" state |N0>+|0N>. Essentially, the grouped N photons of wavelength lambda behave like one photon of wavelength lambda/N. In comparison to a laser beam containing on average N photons, this concept offers an improvement in resolution of square root N. | 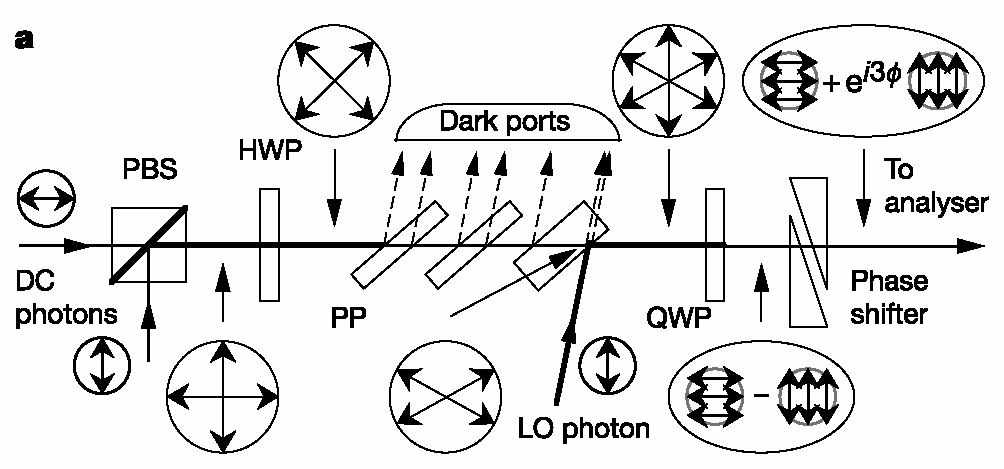 |
| In
comparison to a laser beam
containing on
average N photons, this concept offers an improvement in
resolution
of square
root N. Typically to create this state from unentangled
photons
one
requires strong nonlinearities at the single-photon level.
We
create
our three-photon state from unentangled photons without
strong
nonlinearities by using a generalizable technique that
combines linear
optics transformations with post-selection. For this reason,
this could
be extended to arbitrary
resolution improvement with some future advances in
single-photon
production. In general this work has possible ramifications
for a
variety of resolution- and/or sensitivity-limited
measurements.
Specific applications of this state have been suggested for
spectroscopy, precise metrology, and optical lithography. |
 |
Does a which-way measurement kick the particle?
Young's double-slit revisited.
| The double-slit was one of the first experiments with which scientists realized that quantum mechanics has some very odd properties. In particular, when a particle has a chance of travelling through two slits, the particles always arrive at a screen on the other side in a peculiar pattern. This pattern is set of parallel lines, like the teeth of comb. However, if there is any way of knowing which slit the particle travelled through these lines disappear, replaced with the pattern one gets with a single slit (containing no lines). Bohr said this is because whatever device you used to measure which slit the particle went through also gives the particle a little kick, blurring out the lines. This became to be known as the Heisenberg uncertainty principle. Einstein came up with many ingenious attempts to try and avoid this fact but in the end failed. In the 1990s, Marlan Scully and coworkers seemed to finally come up with measurement device that got around Bohr's rule. It was controversial and nobody could directly test whether it kicked the particles or not. This is where our experiment comes in. See the amusing video to the left for more information about the famous Young's double-slit experiment. |
|
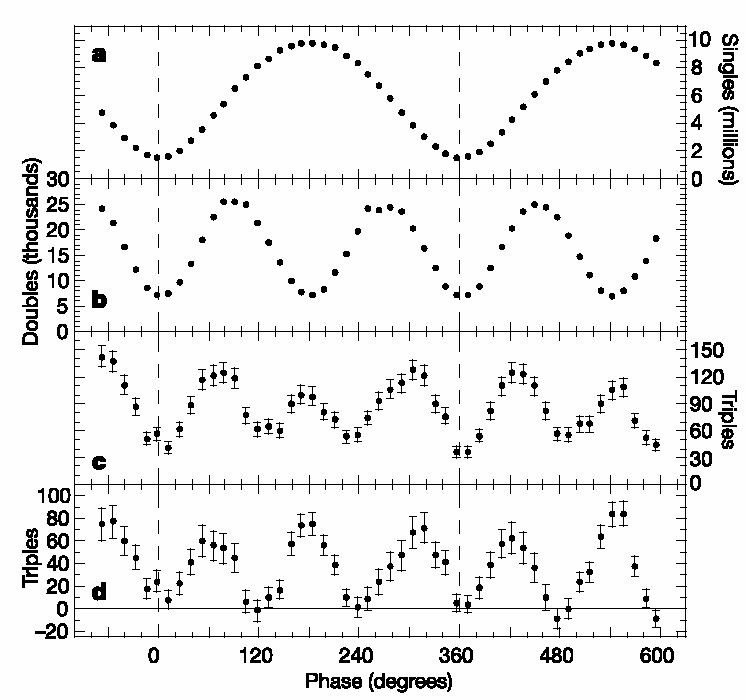
| This paper addresses the longstanding debate over how measurement may destroy interference, which dates back to Bohr and Einstein in the 1920s. It is known that any which-way measurement destroys interference, but it has remained controversial what mechanism enforces this complementarity. In particular, this was debated in the pages of Nature through the 1990s. One camp (Storey et al.) asserted that the mechanism is always momentum disturbance, in accordance with Heisenberg’s uncertainty principle, as Bohr had argued. The other camp (Scully et al.) argued that no such disturbance is necessary, so that complementarity is not enforced by the uncertainty principle. In this paper we present the first measurement of the momentum transfer caused by a which-path measurement. With a tilted glass sliver we weakly measure the momentum p1 of a photon after the double slit. We then do a which path measurement with a half-wave plate (HWP). After, we measure the final momentum p2 of the photons with a CCD camera after a lens. | 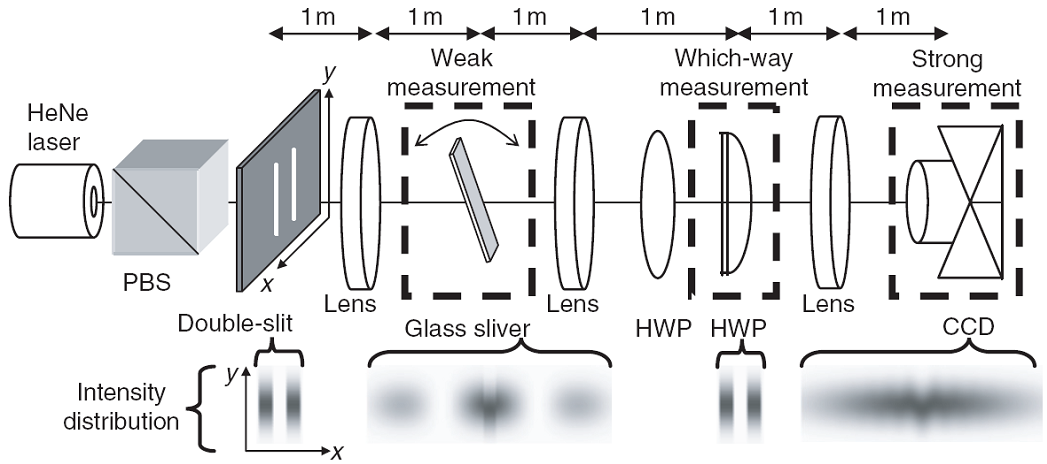 |
| The difference p2-p1=q the momentum transfer. Repeating this many times, we measure the probability distribution P(q) of momentumtransfers q, but find that this distribution is negative for some values of q because of the quantum nature of the momentum transfer. This allows the distribution we measure (a weak-valued distribution) to satisfy theoretical claims made by both sides of the debate: it has a width of order that expected by the uncertainty principle, but has a variance consistent with zero (see figure). Thus our experiment has the potential to reconciles the two camps, by fully demonstrating the connections between three of the most fundamental issues in quantum mechanics: complementarity, measurement, and the uncertainty principle. Moreover, this was done using the archetype of quantum mechanics experiments — Youngs double-slit — which is familiar to all physicists. | 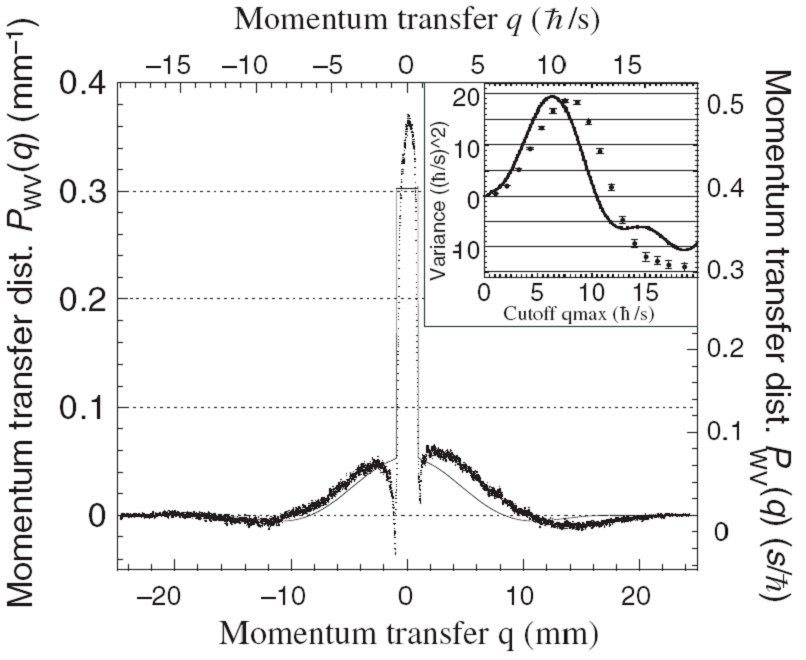 |


 potential to produce light on demand (i.e. triggered) and
a high
repetition rate (i.e. they can be bright). Our InAs dots
are
particularly nice because they are grown (at NRC) on the
top of InP
pyramids. Quantum DotsArrays of these pyramids are
fabricated
giving us quantum dots grown in array of positions, known
to within 10
nm or so. This means the dots can be placed precisely in
the
antinode of an optical cavity. The optical cavities vary
in type but we
use 2-d photon crystal cavities. These are an array of
holes, drilled
into InP. This structure is made to inhibit optical
emission of the
quantum dot. A defect in the structure then acts as a
cavity, capturing
the emitted single-photons and, with careful design,
channeling them
towards an optical fiber. From that point we can use these
photons as
carries of information and, in the future, use them to
build quantum
computers or in quantum cryptography. The picture shows a)
an array of
dots on a ridge, b) a single dot on top of pyramid, c)
electrical
gates isolating a single dot on the ridge, d) a pyramid
with gates on
it. The gates allow us to manipulate the levels and, thus,
the emission
of the dot.
potential to produce light on demand (i.e. triggered) and
a high
repetition rate (i.e. they can be bright). Our InAs dots
are
particularly nice because they are grown (at NRC) on the
top of InP
pyramids. Quantum DotsArrays of these pyramids are
fabricated
giving us quantum dots grown in array of positions, known
to within 10
nm or so. This means the dots can be placed precisely in
the
antinode of an optical cavity. The optical cavities vary
in type but we
use 2-d photon crystal cavities. These are an array of
holes, drilled
into InP. This structure is made to inhibit optical
emission of the
quantum dot. A defect in the structure then acts as a
cavity, capturing
the emitted single-photons and, with careful design,
channeling them
towards an optical fiber. From that point we can use these
photons as
carries of information and, in the future, use them to
build quantum
computers or in quantum cryptography. The picture shows a)
an array of
dots on a ridge, b) a single dot on top of pyramid, c)
electrical
gates isolating a single dot on the ridge, d) a pyramid
with gates on
it. The gates allow us to manipulate the levels and, thus,
the emission
of the dot.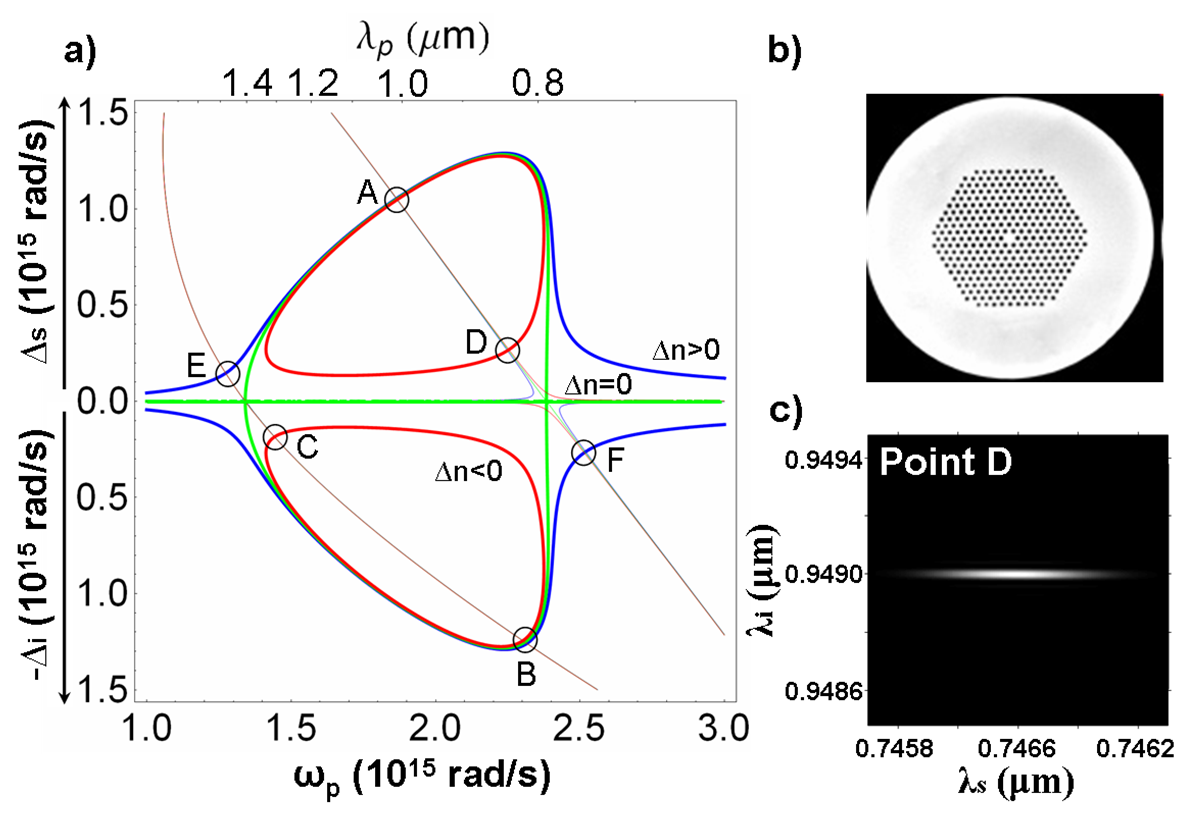 conservation.
There are exciting
opportunities to apply the same techniques in other
systems,
particularly microstructured waveguide
systems, where dispersion (and thus the photon momentum)
is controlled
via the structure, or atomic sources where dispersion is
controlled via
ancillary lasers (e.g. slow light). These new systems hold
the promise
of quantum
light sources with flexible spectral, spatial and
entanglement
properties. On the right is a) Energy-momentum
conservation curves for
photon-pair (signal, s, and idler, i) generation in the
photonic
crystal fiber shown in b) for positive, zero, and negative
birefringence (red, green, blue) and pump frequency ω_p.
Points A to F
bound regions along the curves in which spectrally pure
photons can be
generated. c) The theoretical joint spectrum of the photon
pair at
point D.
conservation.
There are exciting
opportunities to apply the same techniques in other
systems,
particularly microstructured waveguide
systems, where dispersion (and thus the photon momentum)
is controlled
via the structure, or atomic sources where dispersion is
controlled via
ancillary lasers (e.g. slow light). These new systems hold
the promise
of quantum
light sources with flexible spectral, spatial and
entanglement
properties. On the right is a) Energy-momentum
conservation curves for
photon-pair (signal, s, and idler, i) generation in the
photonic
crystal fiber shown in b) for positive, zero, and negative
birefringence (red, green, blue) and pump frequency ω_p.
Points A to F
bound regions along the curves in which spectrally pure
photons can be
generated. c) The theoretical joint spectrum of the photon
pair at
point D.